تفسير حلم الزواج للعزباء
تفسير رؤية الوضوء في المنام لابن سيرين
تفسير رؤية الضرب في المنام
رؤية البحر في المنام لابن سيرين
تفسير رؤية القطط في المنام للفتاة العزباء
رؤية الثعبان في المنام لابن سيرين
تفسير رؤية النمل في المنام
تفسير رؤية الاستحمام في المنام
معاني ألوان الورود بالتفصيل
تفسير رؤية القتل في المنام
تجربتي مع حبوب بانتوجار للشعر
طريقة عمل كبدة الخروف
طريقة عمل الكنافة في البيت
تفسير رؤية البكاء في المنام لابن سيرين
تفسير رؤية التمر في المنام لابن سيرين
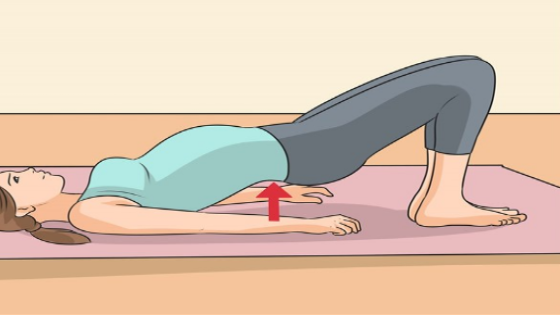
ما هي فوائد التمرين أثناء الحمل؟
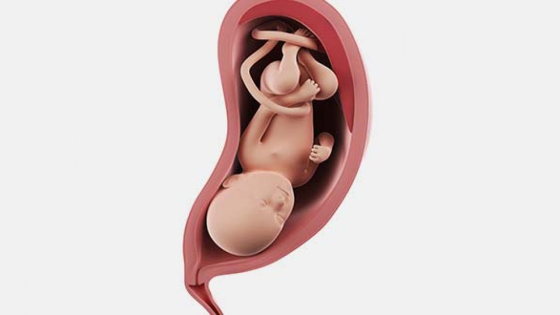
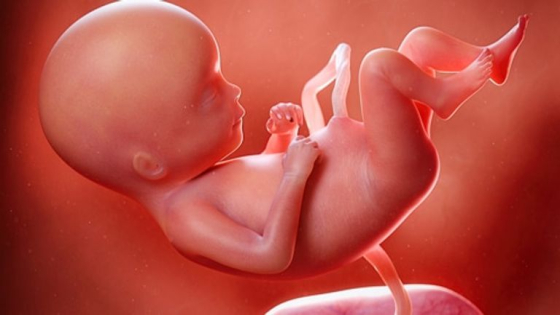
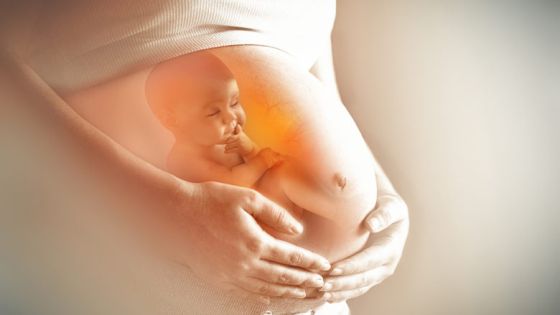
حالة الجنين والأم في الأسبوع الثامن والثلاثون من الحمل
ماذا يحدث للجنين في الأسبوع التاسع والثلاثون من الحمل
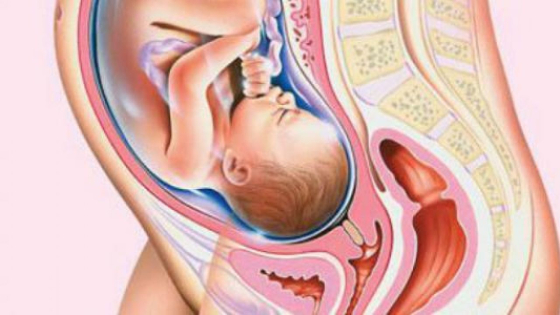
تفاصيل الأسبوع الثاني والثلاثون من الحمل
الحالة الصحية في الأسبوع الثالث والعشرون من الحمل للجنين